Teaching fraction comparison is difficult. It ranks right up there with estimation and measurement as a topic that many math teachers would rather see just go away. If I’m honest with myself, my attitude towards comparison lessons was always to set my teeth and just “make it through.” We might not say it out loud often, but math teachers find fraction comparison and ordering to be one of the hardest topics to teach well! However, this is a real problem because fraction comparison is actually hugely important for students.
Understanding fraction magnitude is an essential part of fractions learning
If we can give our students a flexible and robust understanding of fraction magnitude (size), they can better understand and perform operations with fractions (addition, subtraction, etc.) and evaluate the reasonableness of their answers.
Not only that, but research increasingly demonstrates a link between comparison skills and algebra, with one study concluding that “students who have a stronger understanding of fraction magnitudes when they begin an algebra course learn more of the algebra content than peers who start with weaker fraction magnitude understanding” (Booth, Newton & Twiss-Garrity, 2014, as cited in Rodrigues et al., 2016). Helping our students better understand fractions’ size (and then compare them accurately) actually helps prepare them for the difficulties of algebra!
Bottom line: Gaining solid skills in fraction comparison is good for your students now and crucial for their performance later.
How can I teach my students how to compare fractions?
Okay, I believe you! Fraction comparison is important. But it’s really hard to teach. How can I teach it well? That’s the critical question!
Let’s start with the bad news: there’s no magical solution for making fraction comparison easy. If there were, you probably wouldn’t be reading this article, would you?
As it is, many of us look for the quickest, most pain-free way out of this difficult topic, trying to save our students – and ourselves – heartache. It’s a super understandable thing to do. Everybody finds comparing fractions frustrating:
- Students find comparison work frustrating because they rarely develop the strong number sense around fractions required to compare fractions. Because of that, fraction comparison content that should be within reach isn’t – students don’t have the necessary number sense for the comparison skills to be easily learnable.
- Teachers find it challenging because it’s nearly impossible to dedicate enough class time to building up that missing number sense. Why? Because grade-level standards pre-suppose fraction sense from previous grades, even though it never actually gets built. This creates a snowball effect that seems impossible to stop.
With everyone in the classroom frustrated, no wonder many of us look to shortcuts and “one-size-fits-all” rules to get our students successfully through the content and on to other less time-consuming and frustrating material.
Beware the pitfall of fraction comparison “shortcuts”
However tempting those shortcuts and universal rules may be, relying on them ultimately keeps that snowball effect of “lack of number sense = surface-level learning” rolling for another year.
Here are some shortcuts you’ll hear proposed by folks who are genuinely trying to help teachers and students…and why it’s best to avoid them. Like many classroom shortcuts, even though they’re well-intentioned, in the long run, they ultimately wind up creating more problems for students than they solve. Like any tool, they should only be used for the job they’re meant for!
-
Common shortcut #1: “Turn it into a decimal and move on.” Some teachers tell students simply to “use a calculator, divide each fraction’s numerator by its denominator, and then compare the resulting decimals.”
This shortcut may be good for comparing a fraction with a percent or a decimal, but it’s not at all a good tool for comparing two fractions. Sure, it’s “effective.” It may get your students the right answer on that one comparison question, but it will rob them of a far more important opportunity. This method short-circuits fraction comparison entirely and prevents students from understanding how a fraction’s numerator and denominator work together to create a fraction’s value… ultimately depriving them of critical algebra-readiness skills.
- Common shortcut #2: “Make like denominators and move on.” This shortcut is a tricky one because sometimes it’s the right thing to do in order to compare two fractions. But it’s often not the most efficient way to compare them. Even worse, if your students have learned to rely only on this one strategy, they will have short-circuited the possibility of a much more robust conceptual understanding.
Here’s an example to show you what I mean.
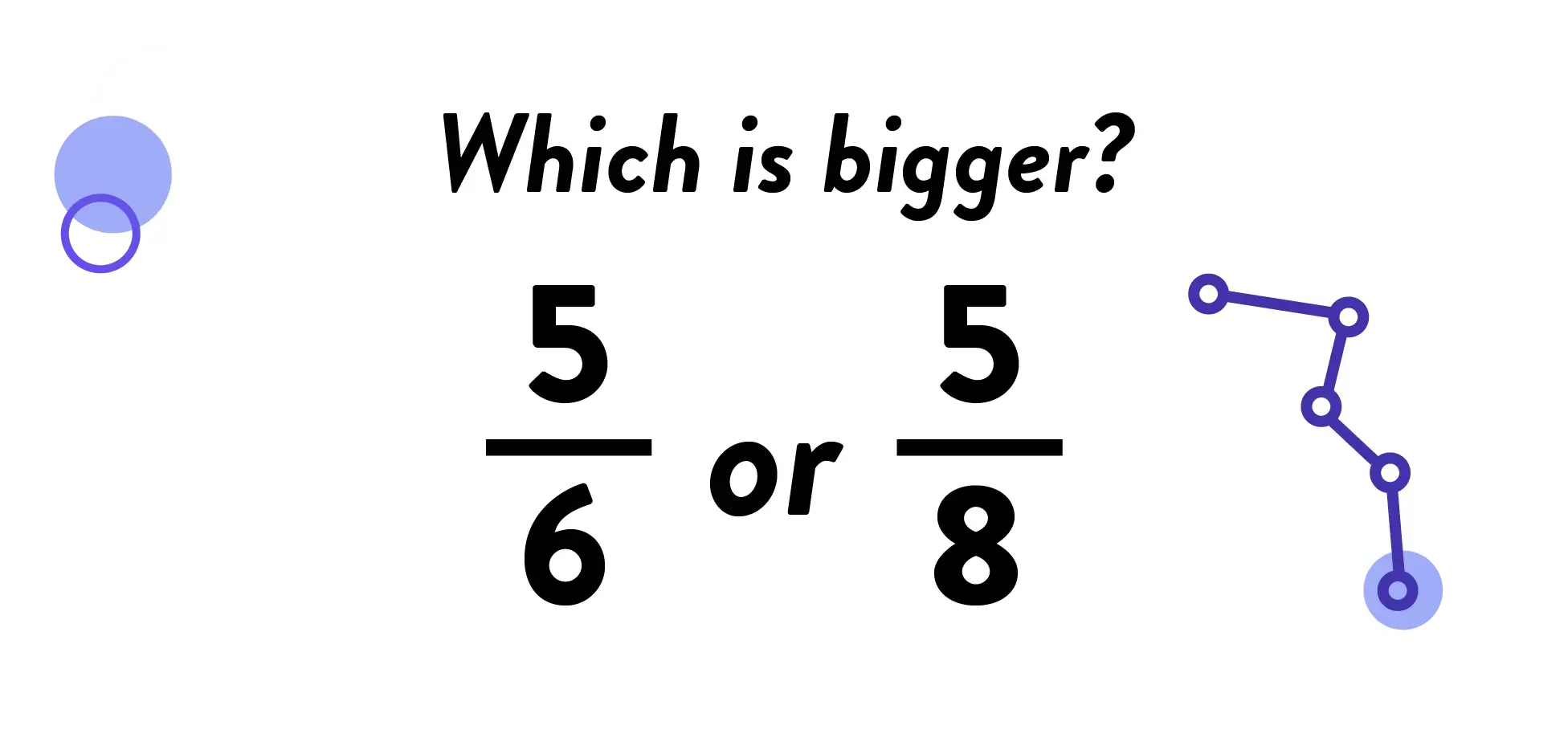
Using the “shortcut,” a student could find a common denominator and make equivalent fractions to compare these two numbers.
In practice, that means the student would have to:
-
Recognize that 24 is the least common denominator. Of course, many students probably wouldn’t see that and instead use 48 as the common denominator (because 6x8=48).
-
Rewrite both fractions as equivalent fractions with that common denominator:
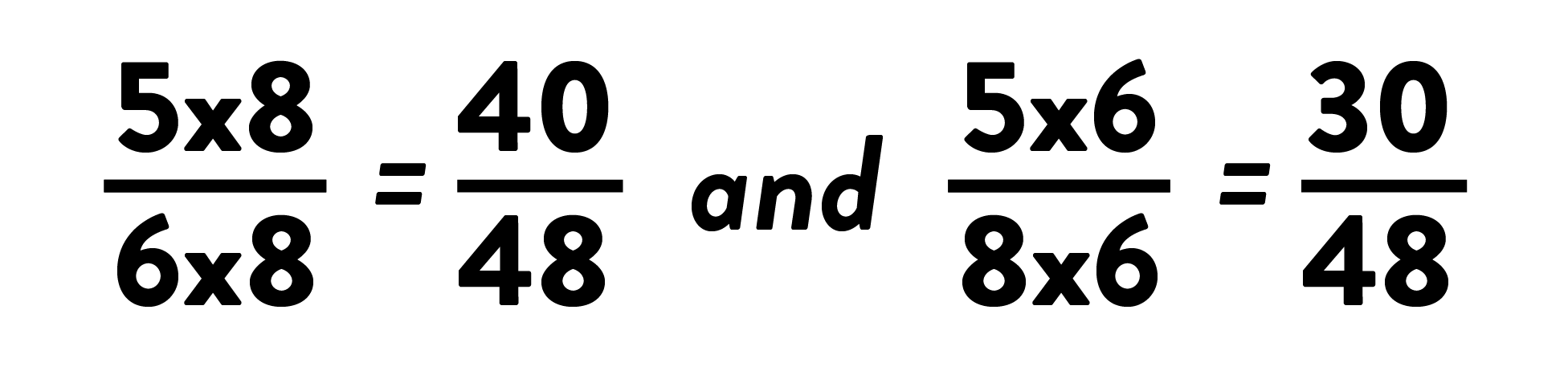
-
Compare the two new fractions:
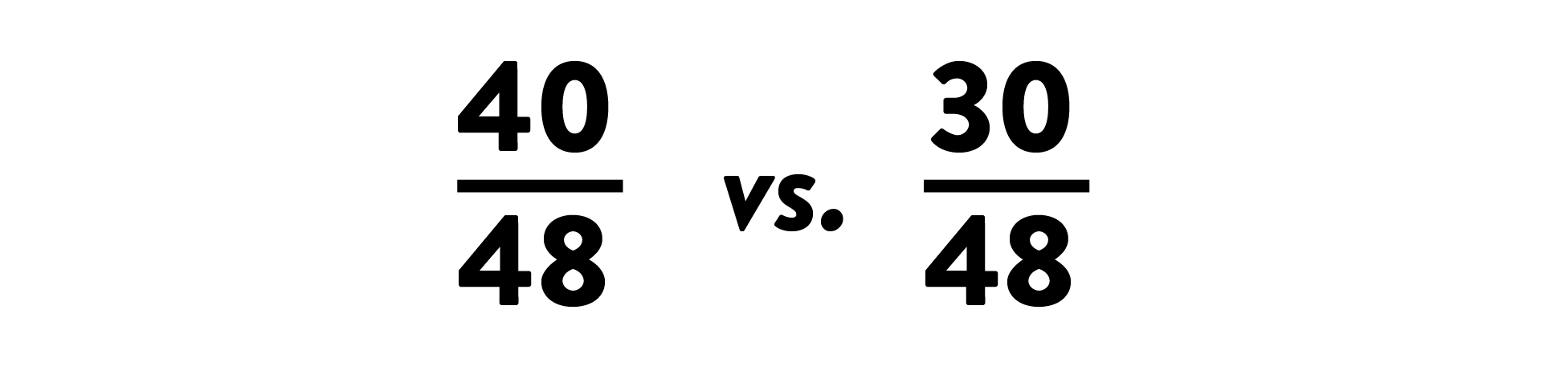
-
Compare 40 and 30 to find the correct comparison (and remember which comparison sign to use):
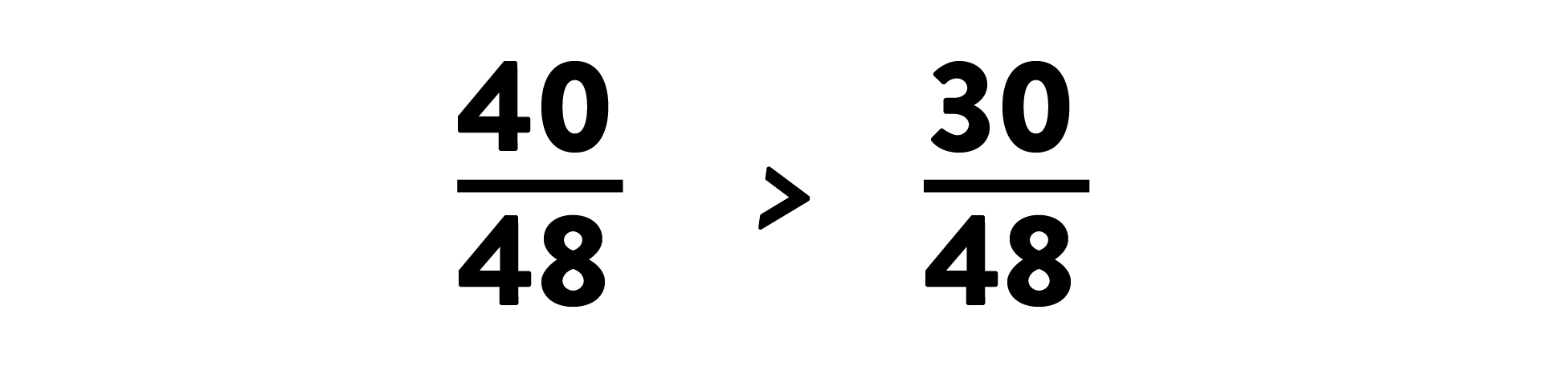
-
Connect the equivalent fractions made back to the ones the student was given to ultimately find the answer:
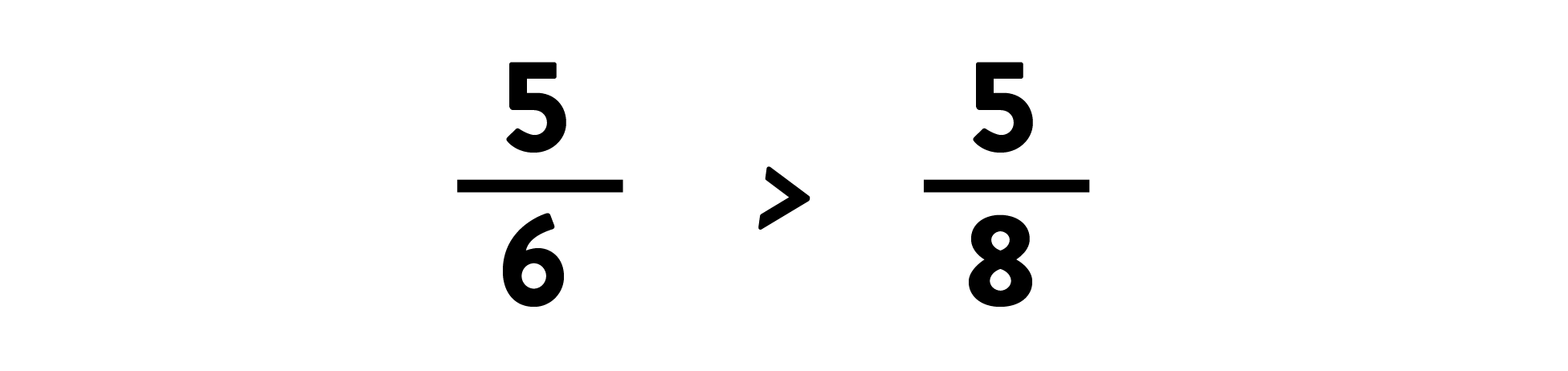
Whew! I’m tired just writing this. Imagine how the poor student must feel…
And that’s one of the main problems with this method: it’s inefficient. It’s also prone to error, especially when the numbers get big, and it hinders otherwise mature conceptual reflection about fractions as numbers in their own right (rather than the subject of arbitrary rules). Not to mention the difficulties this poses for students with attention issues, students whose math fact knowledge is weak, or students who have difficulty retaining multi-step algorithms in their heads.
There are so many ways a student could make a mistake here, and once they do, they’re likely to be completely lost. No wonder so many students find comparison frustrating!
Avoid the shortcuts! Teach fraction magnitude understanding
Now, here’s the good news – fraction comparison can be made easier for your students. When students have built up a robust understanding of fractions as numbers (that is, as a single number with its unique location on the number line), they can learn how to use a variety of approaches to compare those numbers.
Think of it this way. Most of us are very comfortable with the base-10 number system. We see whole numbers and decimals as individual “things,” each with its unique location on the number line closer to (or further from) 0. Having this intuitive understanding allows us to make all of the following comparisons very easily using very different methods:
Comparison A: 10,000 vs. 150
Comparison B: 9,999,999 vs. 10,000,000
Comparison C: 0.2 vs. 2.5
For
Comparison A, you probably didn’t need to think very hard at all. Neither number has a decimal, and 10,000 has several more place values than 150. It’s clearly bigger!
For Comparison C, you also probably didn’t need to stop and think. One of the two numbers is a decimal with a leading zero, meaning it’s between 0 and 1. The other number has a digit in the one’s place. It’s clearly bigger than 1…and thus bigger than the other number.
It’s likely only Comparison B that may have taken any thought or time. You may have needed to stop and count place values to ensure that you were comparing a number in the millions to a number in the ten millions. Some students might even need to stack them vertically, just to be sure.
Fraction comparison can be just as flexible and intuitive for your students as base-10 comparison. With an investment of time in building magnitude understanding, your students will develop strategies for comparing fractions and be able to do exactly the same type of reasoning with different types of fraction comparison problems.
For example:
Comparison X: 4/7 vs. 5/7
Comparison Y: 1/3 vs. 3/4
Comparison Z: 5/6 vs. 5/8 Remember this one?
If your only strategy is “find a common denominator and compare,” then
Comparison X is your only friend in this problem set. The rest will take a while, so buckle up – and get ready for a bunch of student errors based on attention, math fact fluency, and more.
The good news is that there’s another way to think about these comparisons for
students who have developed a strong sense of fraction magnitude. Here are some examples of student reasoning.
Student 1: “Comparison X is easy! Both fractions are in sevenths. 5/7 has more sevenths than 4/7, so it’s clearly bigger!”
Student 2: “Comparison Y is a cinch! I just know that 3/4 is bigger than 1/3.” This student might not verbalize it, but she’s developed enough magnitude understanding to have a mental representation of 1/3 as a number close to 0, whereas 3/4 is not far from 1. This means 3/4 is clearly bigger for her. She sees it in her head – no equivalent fractions required!
Student 3: “Nice try, but you’re not going to trick me! I see that Comparison Z has two numerators that are the same. That means that you’ve got five sixths and five eighths. Sixths are bigger than eighths, so clearly, 5/6 is bigger!”
Did any of these make you tired? Me either. Did any of the ways these students verbalized their reasoning make you feel excited and energized as a math teacher? (Yeah, me too.)
And the best part? These students are on their way, not only toward a more robust understanding of fractions, but full-on algebra readiness. Bring on the challenge!
Frax helps students build fraction magnitude understanding quickly and efficiently
The even better news is that a tool exists to help your students gain fraction magnitude understanding in a short amount of time (all while having fun).
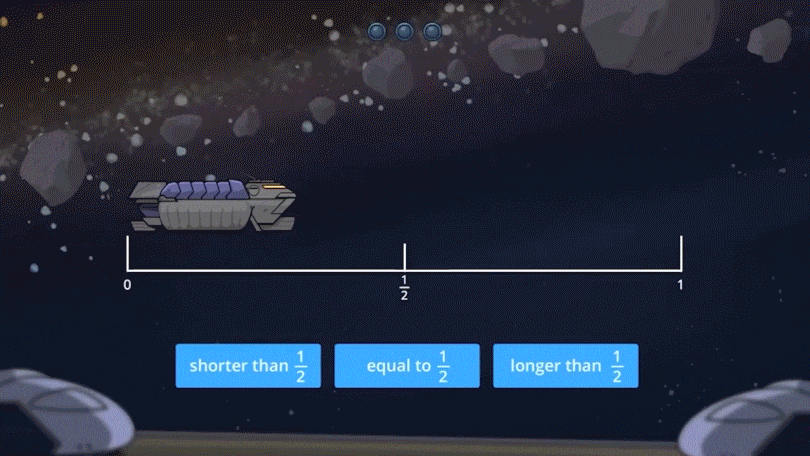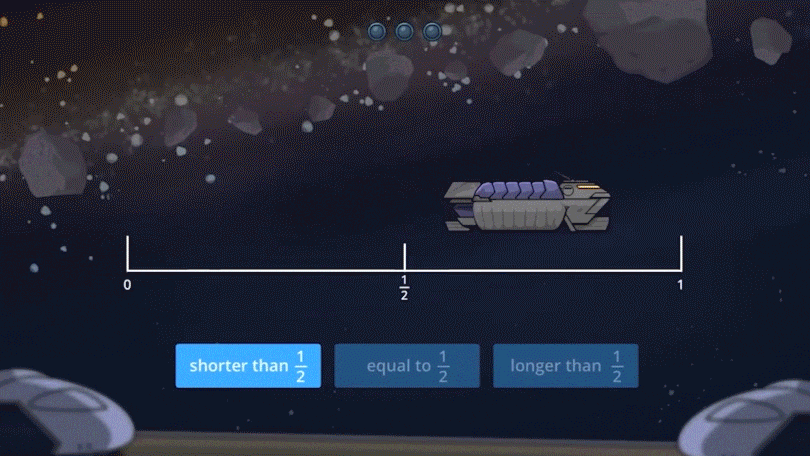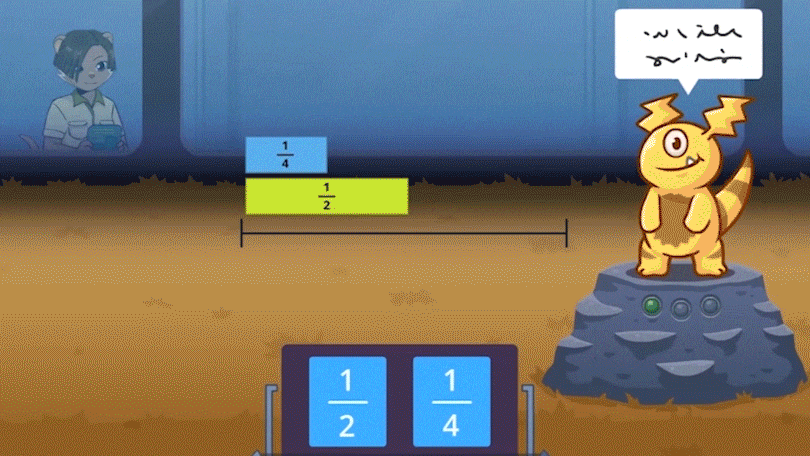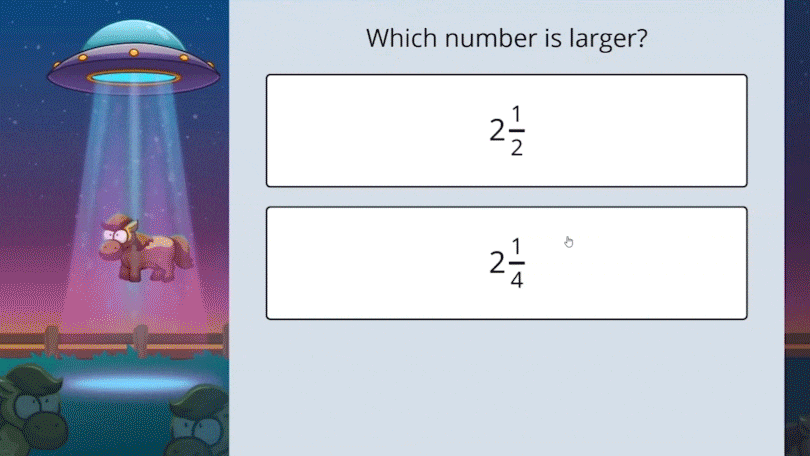
ExploreLearning Frax helps grades 3-5 students develop this kind of robust, flexible knowledge of fraction magnitude. From Day 1 of Frax, students build their understanding of fractions as numbers.
Engaging, game-based instruction uses intuitive representations (like block models) to help students develop a conceptual understanding of magnitude.
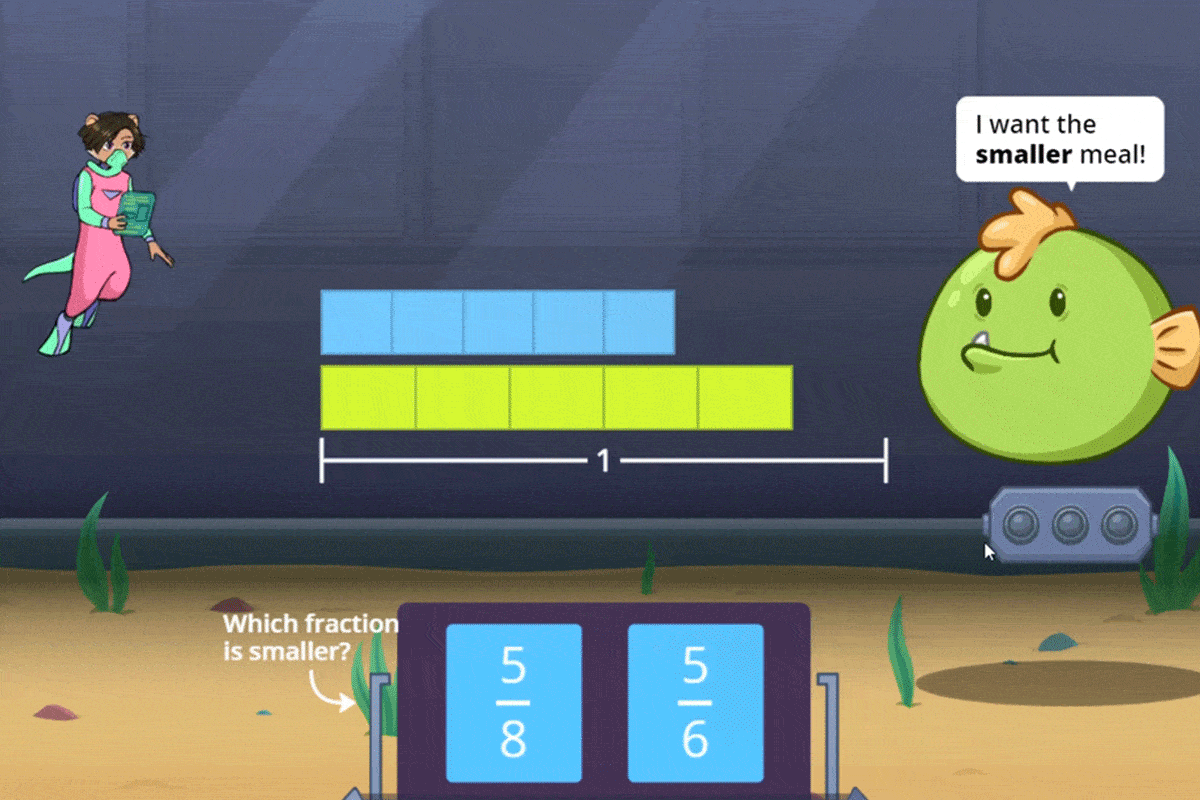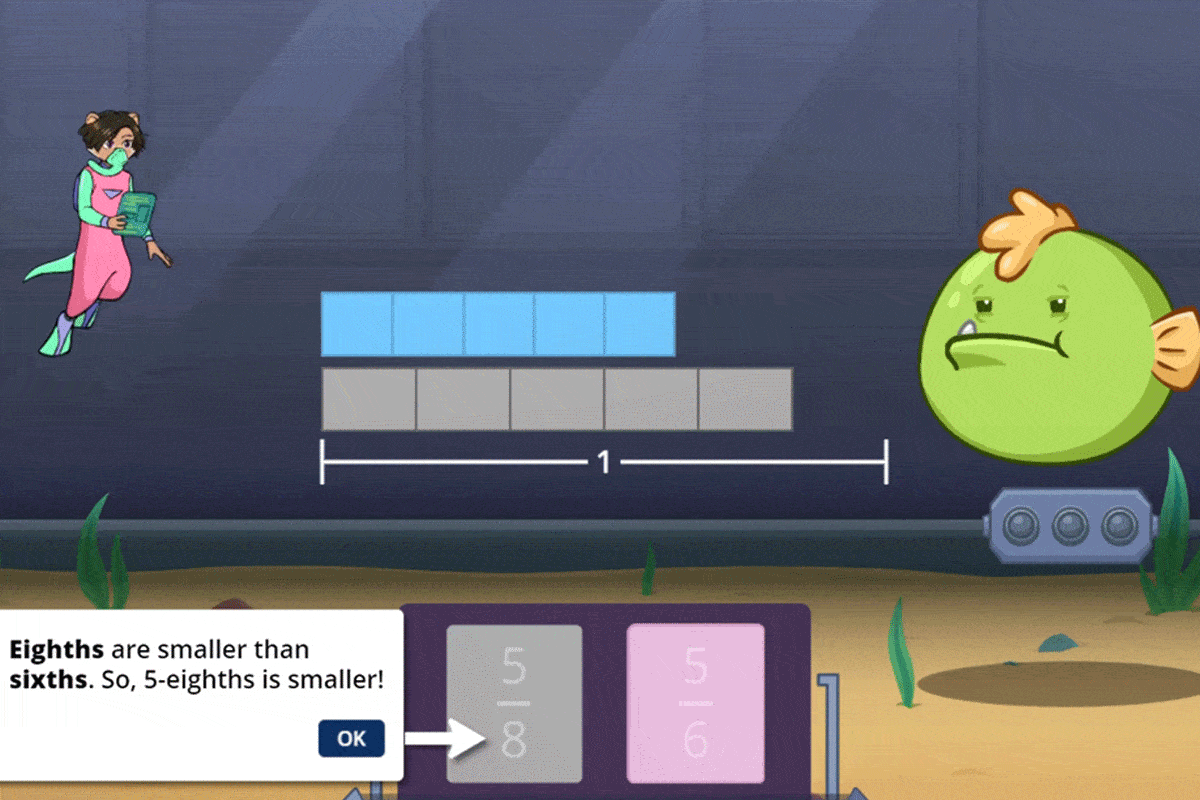
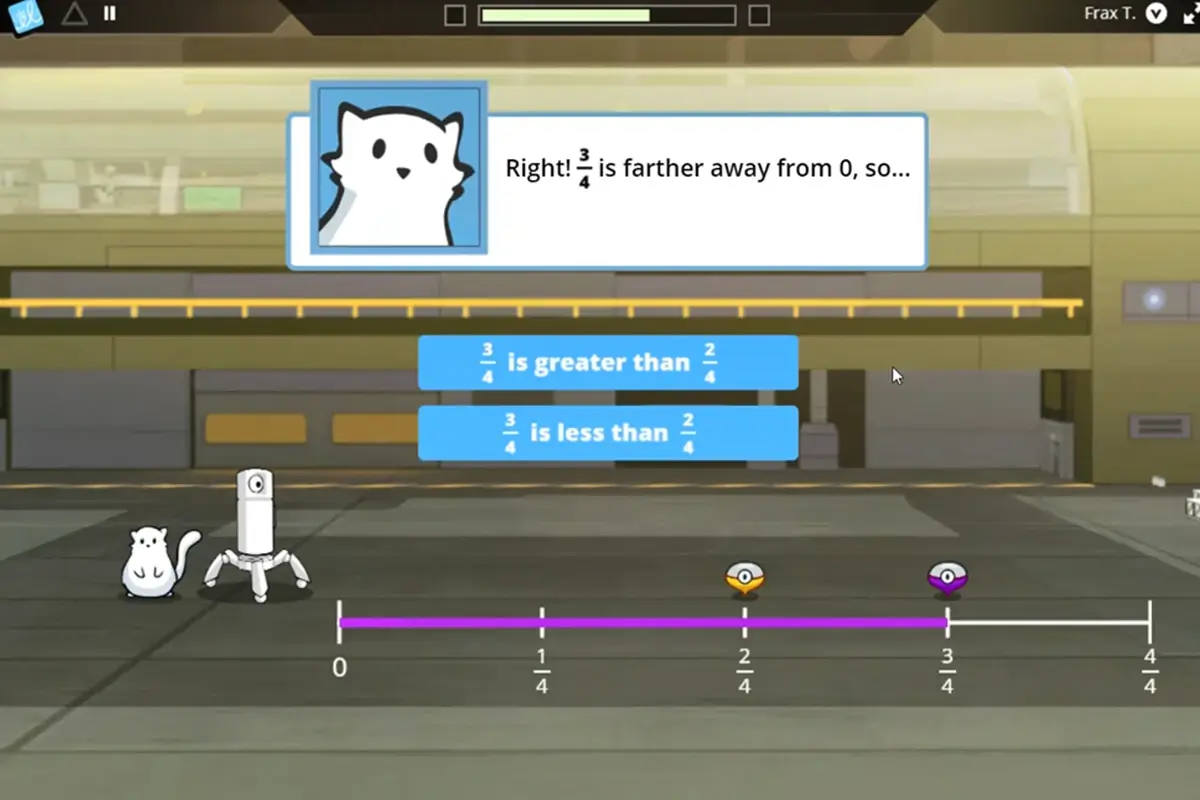
As they mature in their confidence and understanding, students transition gently to the more powerful
number line representation of fractions, coming to understand fraction magnitude as both length and distance from 0.
Almost every Frax lesson contains spiraling practice on magnitude estimation and comparison, so by the time students complete their grade level content, magnitude comparison has become second nature.
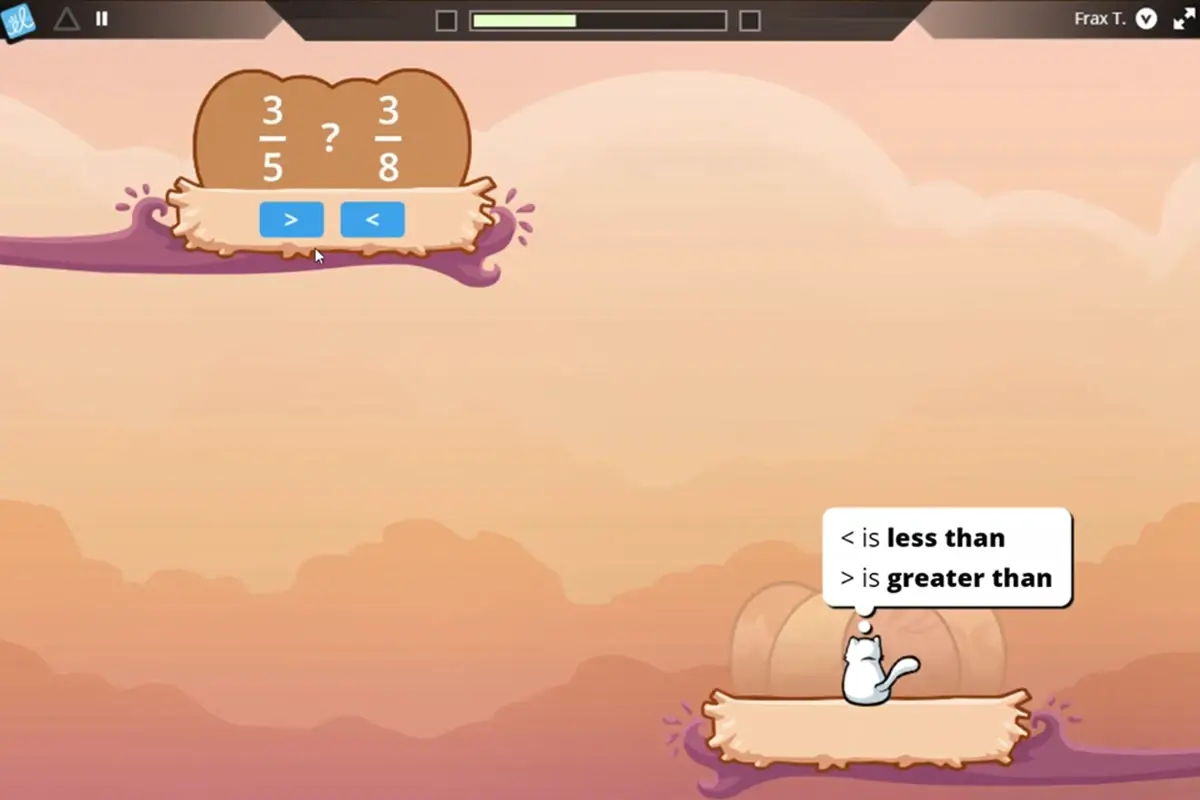
Ultimately, students learn how to use like denominators to make fine-grained comparisons.
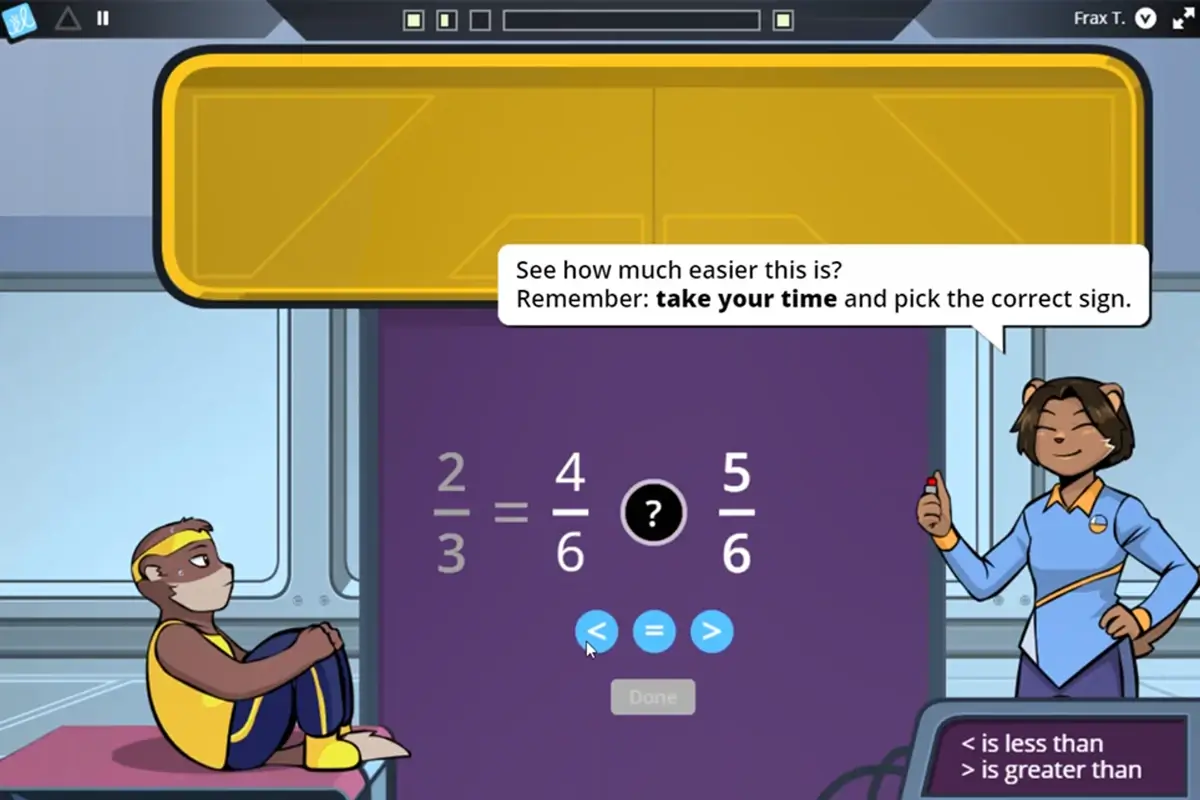
This leads all students to develop a robust set of comparison skills that can be leveraged for quick and easy fraction comparisons in various contexts!
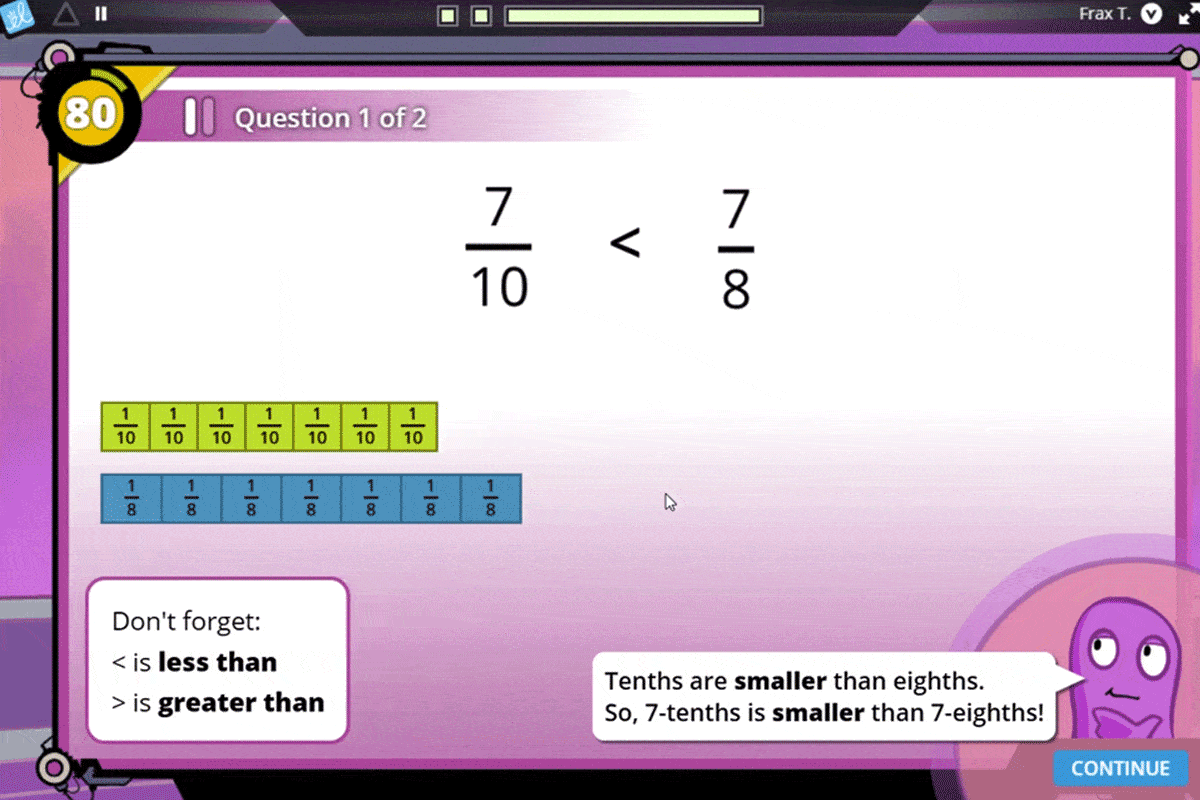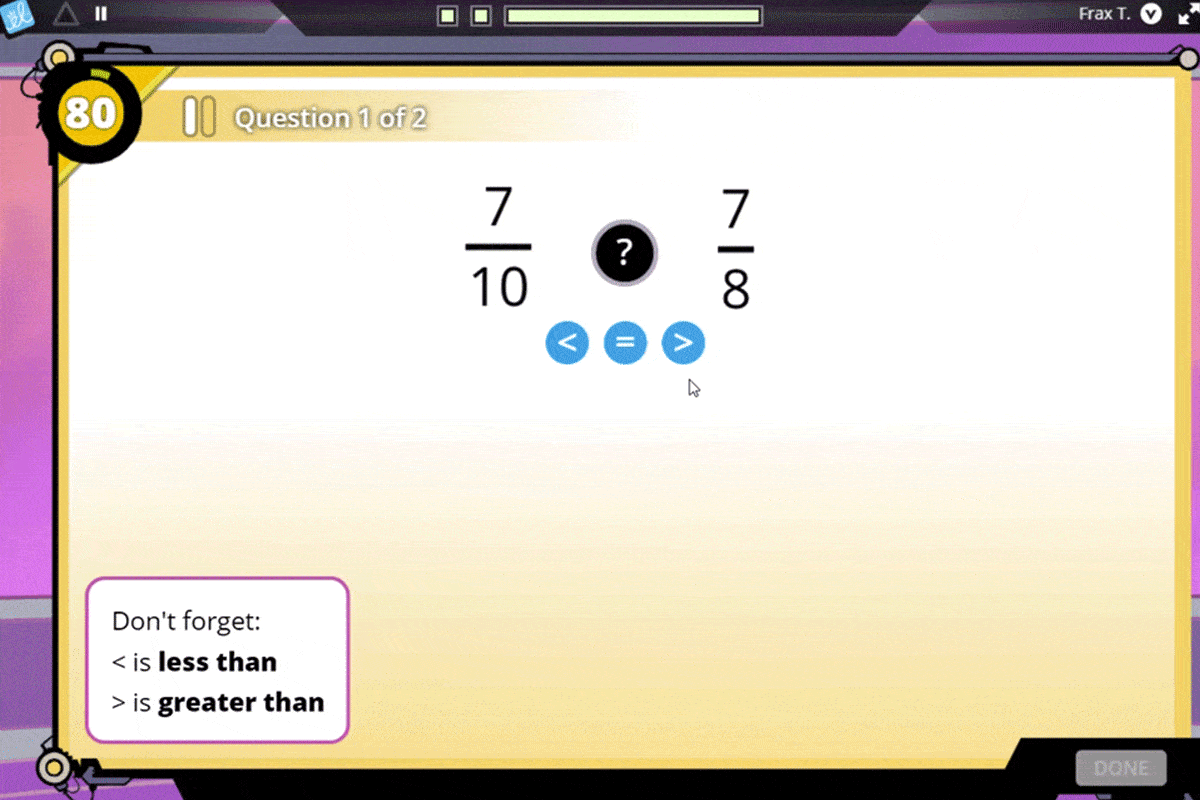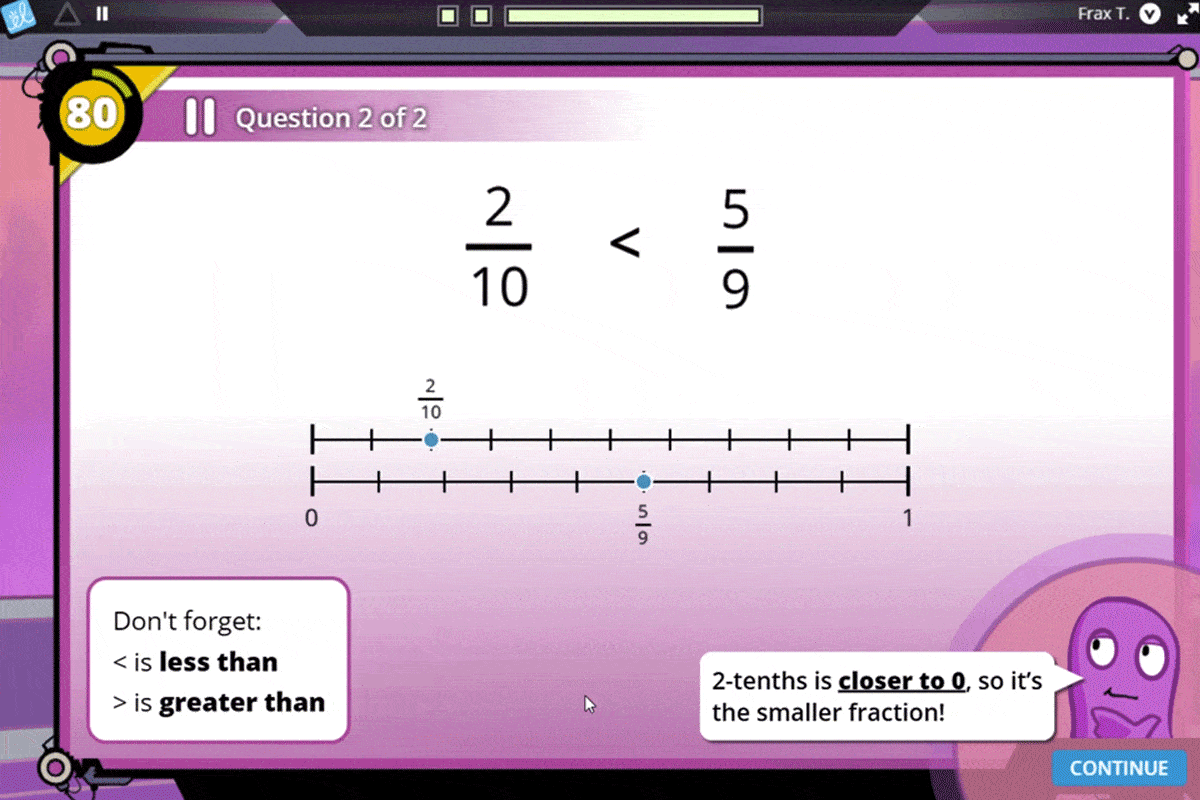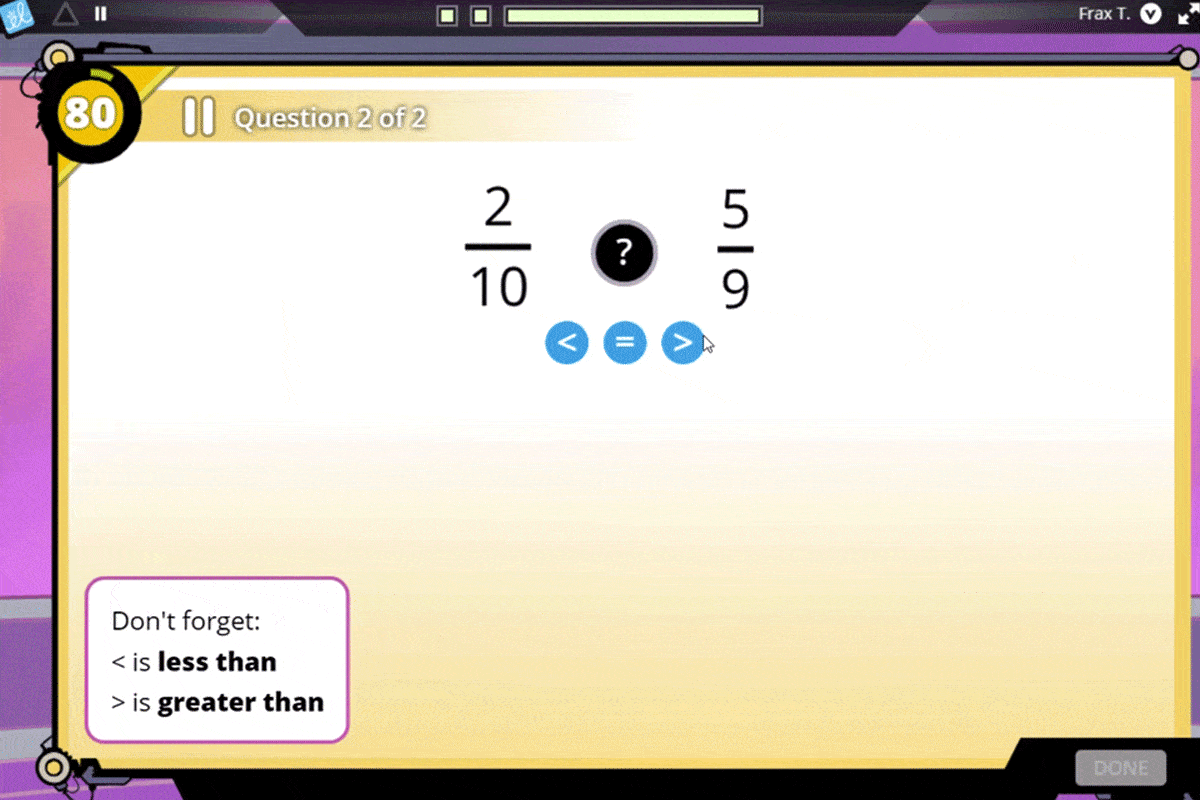
Help your students develop a strong understanding of fraction magnitude to compare fractions.

About the author:
Jesse Mercer, a Senior Product Designer at ExploreLearning, has over 20 years of experience in education and related fields. He has an MA in Math Education, is a National Board Certified teacher for secondary mathematics, and was a recipient of his district’s “Golden Apple” award for teaching. During his 13 years in the classroom, Jesse taught upper elementary and middle school mathematics courses, ranging from 5th-grade math through Algebra I. He currently works with several other designers on creating the curriculum and instructional content for Frax.